どうもコンマスです。早速理論やっていきましょう。
今回は音程のお話。ピッチのことじゃありません。
音程とは:二つの音の間の幅のこと です。
ドとミの音程とか、レとソの音程みたいな言い方をします。
覚えなくてもできないことはないですが、覚えるとかなり楽で、理解も早いので、覚えましょう。
まず、音程は、1度、2度・・・と 度という単位で表します。
度はカンタンに数えられます。ドとドを1度とします。ドとレだったら2度。ドとミだったら3度。ドとファなら・・・もうわかりますね。楽譜上で数えた数がそのまま数字になります。#♭関係なく。
このときに基準にする音をルート音といいます。
上のやつは、ドを基準つまりルートとしています。(ドとミで、ミをルートにしたらミとド、6度となります。)
でもこれ、無限に続いてしまいますよね。ですが実際に使うのは13度くらいまでです。
さらに、この後とっても便利な技を紹介するので、実際覚えるのは5度くらいまででも十分です。(今の時点ではさっぱりで結構です。)
ですが、実際の音程は、○度というだけでは表しきれません。
ドとミ=3度、ドとミ♭=3度
・・・おかしくありませんか?ドとミ ドとミ♭。 音の幅は同じではないことはわかりますね。でも、同じ3度となってしまいました。
これを解決するため、頭に説明をつけて表します。実際は、
ドとミ=長3度 ドとミ♭=短3度
と表します。頭に、長・短をつけます。ドとミのほうが幅が広い(半音4つ分)ので長です。長音程は明るい響き(メジャー)がします。
短3度(半音3つ)は暗い響き(マイナー)です。
2度でも同様です。
ドとレ=長2度(半音2つ) ドとレ♭=短二度(半音)
となります。
1度、4度、5度8度は例外です。
ドとド=完全1度、ドとファ=完全4度(半音5つ)、ドとソ=完全5度(半音7つ)、ドと上のド=完全8度(オクターブ)
となります。 完全ってなんですか。笑ドとファがもし、長4度とか短4度なる音程だったとしてしまうと、矛盾が起こってしまうので、完全とおいたのです。(解説は省略します。覚えてしまってください。)
6度も同様。
ドとラ=長6度、ドとラ♭=短6度
7度
ドとシ=長7度 ドとシ♭=短7度
ここでこの画像を見てください。
この画像は、Cメジャースケール上の音で、Cをルートにして度数を考えた楽譜です。
そう、Cメジャースケール上でCをルートにして度数を考えると、長か完全になるんです。
ここで、便利な技を紹介しておきましょう。
音程の法則
①度数に7を足しても同じ
ex.長2度=長9度(ドとレ=ドと上のレ)完全4度=完全11度(ドとファ=ドと上のファ)など
これをつかえば、11度とかは覚える必要がなくなります。
②足して9となるように度数を入れ替え、長と短を入れ替えてもよい
わかりにくいかもしれないですが、
ex.長3度=短6度(ドとミ=ミとド)
さっきチラっと言いましたが、ドとミを考えるとき、ドをルートとすればミは長3度で、ミをルートとすればドが短6度となる、という要領です。
また、完全音程の場合は、完全4度=完全5度(ドとファはファとド)というように、完全のまま度数のみ入れ替わります。
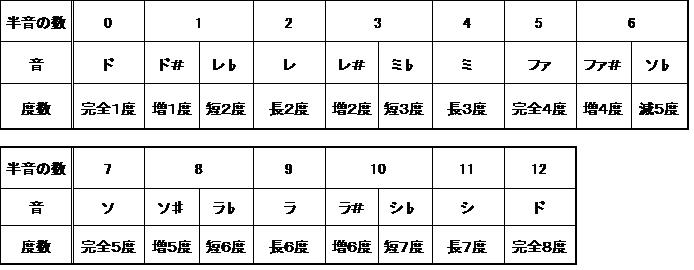
さあ、ごっちゃりしてきたので、表にまとめてみましょう。
これは、ルートをドにしたときの度数の表です。この表のように、度数を半音の数で数える方法もあります。暗記的ですが、先ほどの法則を使えれば、そこまで大変ではないですね。
さあ、見たことがないのがいくつかありますね。増・減です。
特に、ドとファ#、ドとソ♭は先ほど飛ばしたものですが、増4度、減5度となっていますね。
この様な感じです。
増4度はもともとドとファであったが、ファが#したことを表します。
逆に減5度はもともとのドとソの、ソが♭したことを表します。
同様に考えれば、 ドとミ#が、増3度である、ドとミ♭♭が減3度であることなどもわかると思います。
すっごく複雑になってしまって意味不明になってしまいそうなので、まとめてしまいます。
この次に繋がるコードという形で使うのは、
・ルートと完全5度(ex.ドとソ)・・・コードの基本となる。
・3度・・・長3度(ミ)・短3度(ミ♭)・・・コードのメジャー(明るい)・マイナー(暗い)を決める。
・7度・・・長7度(シ)・短7度(シ♭)・・・コードを装飾したり役割付けする。(セブンス)
・9度、11度、13度など(法則で導き出せる)・・・さらに飾り付けする。(テンション)
という具合です。これらが組み合わさって、コードができあがります。